Kim NaRae

배울때마다 기록해두기

1. 해시 테이블

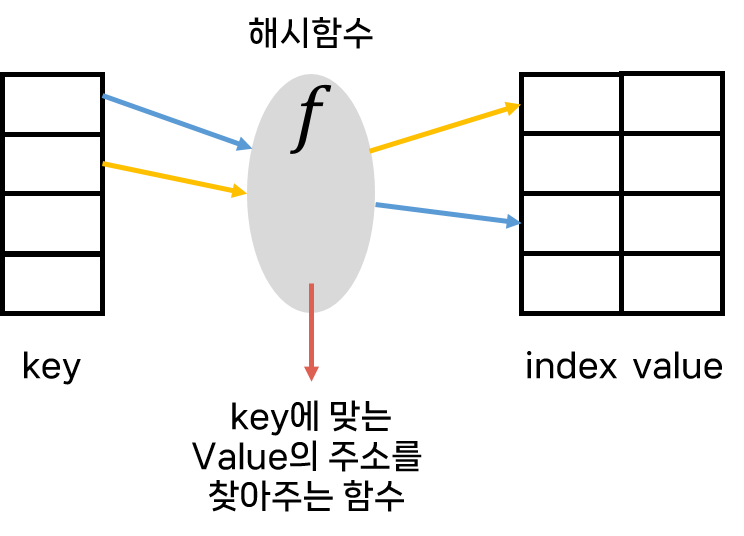
1) 개념 정리

  • key:value 시스템을 이용하여 빠르고 효율적으로 문제를 해결할 수 있다. python에서는 딕셔너리를 이용하여 푸는 것이라고 생각하면 된다.

  • 왜 빠를까? 위의 그림을 보면 해시 함수가 key를 value로 연결 해주는 기능을 한다. 그래서 하나씩 탐색해야 하는 선형리스트보다는 훨씬 빠르다고 할 수 있다.

    시간복잡도($O_n$)으로 알아보기

    • 선형 리스트 : $O(n)$
    • 해시 테이블 : $O(1)$
  • Tips
    • 검색해야 하는 문제인 경우, for loop가 여러번 필요한 경우에는 해시 테이블을 생각하는 것이 좋다.
    • 특히 원소를 찾는 데에 리스트보다 딕셔너리의 key에서 찾는게 더 빠르게 찾을 수 있기 때문에 value에 의미가 없더라도 사용하는게 좋다.

2) 진짜로 빠를까?

value를 탐색하지 않고, key에 있는지를 탐색하는 문제였는데도 효율성 문제 때문에 해시를 사용했었다. 그래서 선형 리스트에서 값을 찾는 것과 해시 테이블의 키에서 값을 찾는 데 $n$이 늘어날수록 시간차이가 있는지 알아보고자 했다.

import random
import time

phone1 = [random.randint(0,100000) for _ in range(20)]
phone2 = {random.randint(0,100000):0 for _ in range(20)}


ns = [1e+03, 1e+04, 1e+05]
for n in ns:
    print(f'n = {n}')
    phone_book = [random.randint(0,100000) for _ in range(int(n))]
    
    # 선형 리스트
    start = time.time()
    cnt = 0
    for x in phone_book:
        if x in phone_book:
            cnt += 1
    end = time.time()
    print(f'선형 리스트: {end - start}')

    # 해시 테이블
    start = time.time()
    cnt = 0
    for x in phone_book:
        if x in phone2:
            cnt += 1
    end = time.time()
    print(f'해시 테이블: {end - start}')

    print('-'*50)

# Output
# n = 1000.0
# 선형 리스트: 0.003999233245849609
# 해시 테이블: 0.0
# --------------------------------------------------
# n = 10000.0
# 선형 리스트: 0.3987877368927002
# 해시 테이블: 0.001004934310913086
# --------------------------------------------------
# n = 100000.0
# 선형 리스트: 29.457832098007202
# 해시 테이블: 0.0
# --------------------------------------------------

$n$이 커질수록 차이가 엄청나게 커짐을 알 수 있다. 이를 통해 탐색할 때에는 value를 쓰지 않더라도 해시 테이블을 이용해야 한다는 것을 깨달았다.

2. 실습 문제

Reference

댓글남기기

참고