[자료구조] 그래프 구현하기

1. 그래프(Graph)

1) 용어 정리

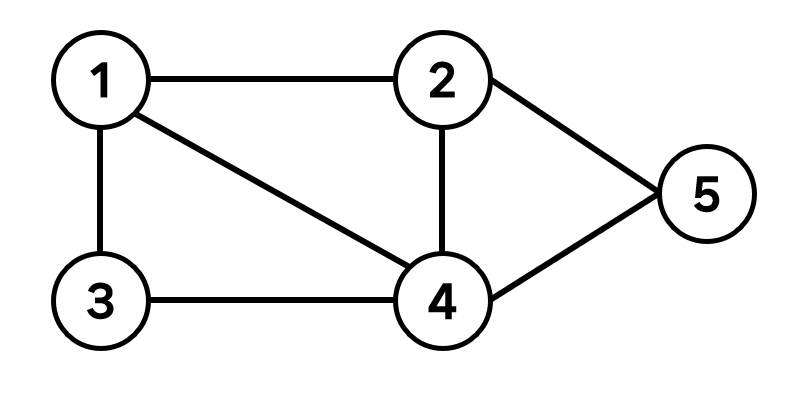
• 정점(Vertex) : 1, 2, 3, 4, 5와 같이 노드(node)를 말한다.
• 간선(Edges) : 정점을 잇는 선을 말한다.
• 인접 정점(Adjacent Vertex) : 한 정점과 이어지는 정점들

수학적 표현

그래프를 $G$라고 하고, 정점과 간선들의 집합을 각각 $V, E$라고 할 때 다음과 같이 표현된다.

\[G = (V,E)\]

위의 그림을 예시로 설명하면 아래와 같은데 이때 간선 정보의 표현은 $(u,v)$라고 할 때 $u<v$를 기준으로 표현했다.

\[\begin{aligned} V &= \{1,2,3,4,5\}\\ E &= \{(1,2),(1,3),(1,4),(2,4),(2,5),(3,4),(4,5)\} \end{aligned}\]

2) 그래프 구조

그래프는 간선의 정보에 따라 3개로 분류할 수 있다.
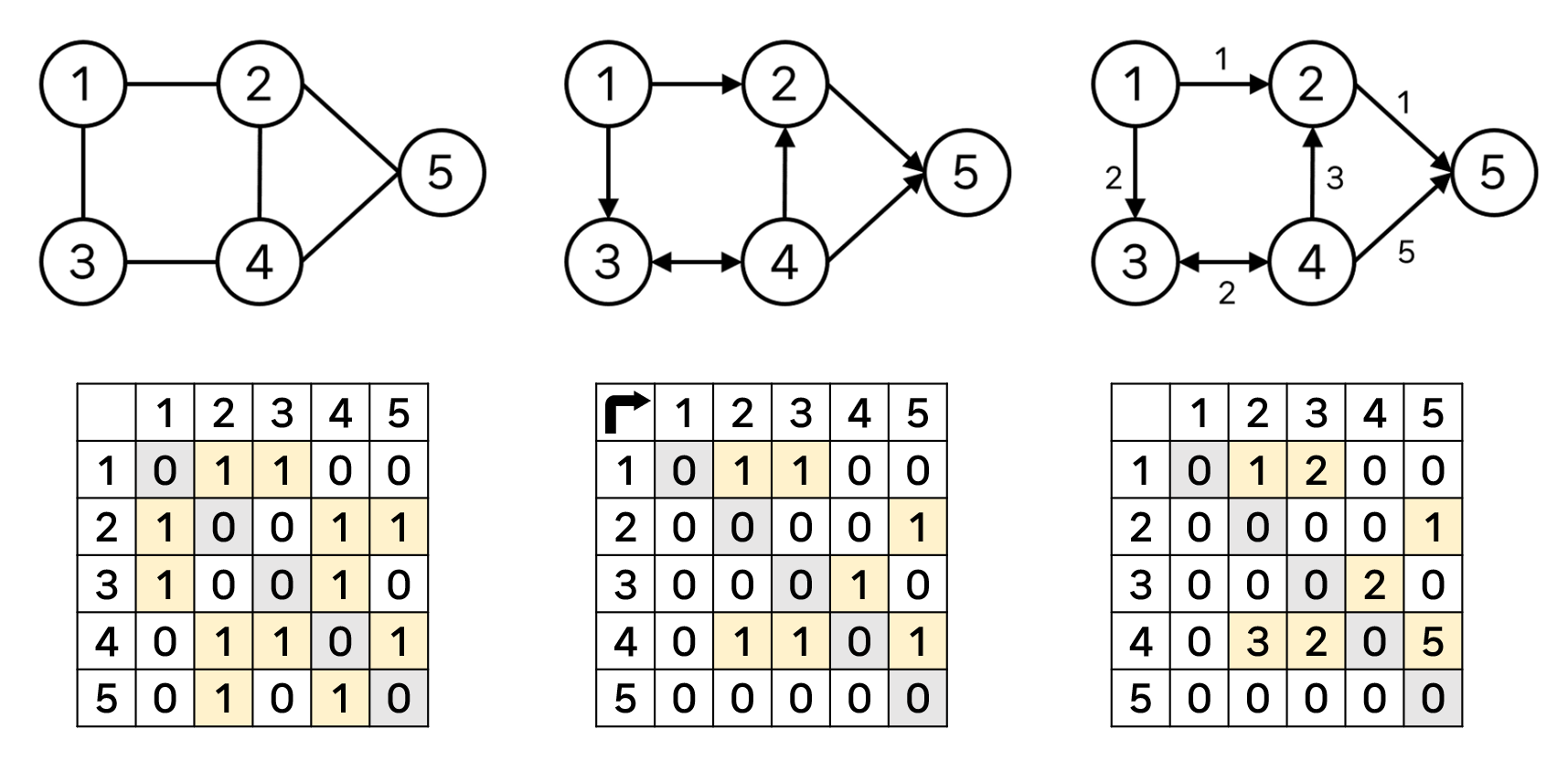
간선에 방향이 없으면 무방향(Undirected), 있으면 방향(Directed), 가중치가 있으면 (Weighted) 그래프라고 한다.

3) 표현 방법(Using Python)

파이썬으로 그래프를 표현할 수 있는 방법은 2가지가 있다. 무방향 그래프인 맨 위의 그래프를 예시로 하여 그려보았다.

인접 행렬(Adjacency Matrix)

정점들의 모든 집합을 행렬로 나타낸 후 간선이 있는 경우를 1로 나타낸 행렬을 말한다. 행렬의 경우 쓰이지 않는 공간이 많아 비효율적인 경우가 많다. 그래서 인접 리스트가 많이 활용된다.

# 노드를 맞추기 위해 0번째 행, 0번째 열을 빈공간으로 해서 표현했다.
def graph_mat(n_vertex, edges):
    graph = [[0 for _ in range(n_vertex+1)] for _ in range(n_vertex+1)]

    for v1, v2 in edges:
        graph[v1][v2] = 1
        graph[v2][v1] = 1
    
    return graph

# Output
# [[0, 0, 0, 0, 0, 0],
#  [0, 0, 1, 1, 1, 0],
#  [0, 1, 0, 0, 1, 1],
#  [0, 1, 0, 0, 1, 0],
#  [0, 1, 1, 1, 0, 1],
#  [0, 0, 1, 0, 1, 0]]

인접 리스트(Adjacency List)

정점들의 인접 정점을 리스트로 표현한 후, 이 정점들을 리스트로 표현한 것을 말한다.
보통 정점은 숫자 1부터 표현되는데 편의를 위해 인접 리스트를 만들 때 0번째 인덱스를 빈 공간으로 나타낸 후 표현한다.
만약 빈 공간으로 표현되는 게 싫다면 딕셔너리로 구현하는 방법도 있다.

# 리스트
def graph_list(n_vertex, edges):
    graph = [[] for _ in range(n_vertex+1)]

    for v1, v2 in edges:
        graph[v1].append(v2)
        graph[v2].append(v1)
    
    return graph

# Output
# [[], [2, 3, 4], [1, 4, 5], [1, 4], [1, 2, 3, 5], [2, 4]]

# 딕셔너리
def graph_dict(n_vertex, edges):
    graph = {i:[] for i in range(1,n_vertex+1)}

    for v1, v2 in edges:
        graph[v1].append(v2)
        graph[v2].append(v1)
    
    return graph

# Output
# {1: [2, 3, 4], 2: [1, 4, 5], 3: [1, 4], 4: [1, 2, 3, 5], 5: [2, 4]}

Reference

• [Wikidocs]좌충우돌, 파이썬으로 자료구조 구현하기