[ML/DL] 선형 회귀분석

October 25, 2022

1. 회귀분석Permalink

종속변수 $Y$ 에 독립변수 $X$ 가 얼마나 영향을 주는지에 대해 분석하는 것.
목적: $X$ 가 주는 영향을 추정하고, 새로운 관측값 $x$ 에 대해 $Y$ 를 잘 예측하고자 한다.

1) 선형 회귀분석 / 비선형 회귀분석Permalink

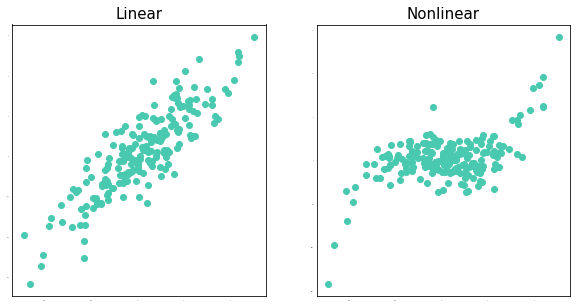
선형 회귀분석Permalink

$Y$ 와 $X$ 의 관계가 선형이라고 가정하고 분석한다.
비교적 단순하기 때문에 구하는 방법이 간단하다.
그대신 가정들이 많다.(오차의 등분산성, 정규성, 독립성 등)
장점: 독립변수 $X$ 가 $Y$ 에 미치는 영향을 해석하기 쉽다..
단점: 실제 데이터는 매우 복잡한 경우가 많아 적용하기에는 어려움이 있다.

비선형 회귀분석Permalink

실제 데이터들의 관계를 보면 선형인 경우는 거의 없기 때문에 이를 반영할 수 있는 분석들이 활발하게 연구되고 있다.
장점: 선형 회귀분석에 비해 실제 데이터를 더 잘 예측한다.
단점: 계산 과정이 매우 복잡하고 $X$ 가 $Y$ 에 미치는 영향을 해석하기 어렵다.

2) 단순 선형 회귀분석 / 다중 선형 회귀분석Permalink

점이 모여서 선이 되고 선이 모여서 면이 되는 것처럼
단순 선형은 설명변수 1개( $x$ )의 조합으로 $Y$ 를 설명하기 때문에 선으로 표현되고,
다중 선형은 설명변수 예를 들어 2개( $x_1,x_2$ )의 조합으로 $Y$ 를 설명하기 때문에 면으로 표현된다.
이때 다중 선형에서 설명변수들의 조합으로 이루어진 공간을 초평면(hyperplane)이라고 한다.

단순 선형 회귀분석Permalink

$y_i = b + ax_i + \epsilon_i,\quad \epsilon_i\overset{iid}{\sim}N(0,\sigma^2),\quad i = 1, 2, \cdots, n$

$a$ 는 기울기(slope), $b$ 는 $y$ 절편(intercept)를 의미한다.

다중 선형 회귀분석Permalink

$y_i = w_0 + w_1x_{i1} + w_2x_{i2} + \cdots + w_Kx_{iK} + \epsilon_i,\quad \epsilon\overset{iid}{\sim}N(0,\sigma^2),\quad i = 1, 2, \cdots, n$

$\begin{bmatrix} y_1\\\ y_2\\\ \vdots\\\ y_n \end{bmatrix}= \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1K} \\\ 1 & x_{21} & x_{22} & \cdots & x_{2K} \\\ \vdots & \vdots & \ddots & \vdots \\\ 1 & x_{n1} & x_{n2} & \cdots & x_{nK} \end{bmatrix} \begin{bmatrix} w_0\\\ w_1\\\ \vdots\\\ w_K \end{bmatrix}+ \begin{bmatrix} \epsilon_1\\\ \epsilon_2\\\ \vdots\\\ \epsilon_n \end{bmatrix}$

행렬로 나타내면 $Y = Xw$ 가 되고,
행렬의 크기는 $(n\times 1)=(n\times(K+1))((K+1)\times 1)+(n\times 1)$ 가 된다.
$w_1, w_2,\cdots w_K$ 는 각 설명변수들( $x_1,x_2,\cdots,x_K$ )가 $Y$ 에 미치는 영향에 대한 크기를 의미한다.
이를 가중치(weight)라고도 부른다.

2. 모수 추정Permalink

단순 선형으로 예를 들어보자. 추정해야할 모수는 2개이다.( $a, b$ )

모수의 추정값이 $a_0, b_0$ 이라고 하자.
추정된 회귀식은 다음과 같다. $\hat{y} = a_0 + b_0x$
모수 추정이 잘 됐는지 확인해야 한다. $\Rightarrow$ 오차( $e = y - \hat{y}$ ) 이용
즉, 실제 $y$ 값과 예측한 $y$ 값의 차이가 작을수록 잘 추정이 되었다고 할 수 있다.
우리는 오차의 크기에 관심이 있기 때문에 평균제곱오차(MSE, Mean Squared Error)를 이용한다.

$MSE = \dfrac{1}{n}\sum_{i=1}^n (y_i-\hat{y})^2 = \dfrac{1}{n}\sum_{i=1}^n(y_i - (b + ax_i))^2$

평균제곱오차(MSE)

Cost Function이라고 할 수 있다. MSE가 작을수록 잘 추정했다고 할 수 있다.

따라서 선형 회귀분석에서 모수 추정은 MSE를 최소화하는 모수를 찾는 것이 목표이다.

그렇다면 이제 어떻게 접근해야 할까?

IDEA! MSE의 식이 모수에 대한 이차식이니까 기울기가 0인 곳이 최소값이 되지 않을까?

설명변수가 한 개일 때Permalink

$MSE(a,b) = \dfrac{1}{n}\sum\limits_{i=1}^n(y_i - (b + ax_i))^2$

$b$ 가 주어져 있다고 할 때, MSE는 $a$ 에 대한 이차식이고,
$a$ 가 주어져 있다고 할 때, MSE는 $b$ 에 대한 이차식이다.

편미분을 하면 다음과 같다.
(상수 2는 나중에 생략한다. 상수가 있든 없든 $i=1,\cdots,n$ 의 오차 크기 순서가 변하지 않기 때문에)

$\begin{aligned} \dfrac{\partial MSE}{\partial b} &= 2\dfrac{1}{n}\sum_i^n -(y_i-(b+ax_i))\\\ \dfrac{\partial MSE}{\partial a} &= 2\dfrac{1}{n}\sum_i^n -x_i(y_i-(b+ax_i)) \end{aligned}$

의미 > $\hat{y}_i=b + ax_i$ 일 때

$\dfrac{\partial MSE}{\partial b}$ : $-(y_i-\hat{y}_i)$ 들의 평균이다.
$\dfrac{\partial MSE}{\partial a}$ : $-x_i(y_i-\hat{y}_i)$ 들의 평균이다.

설명변수가 $K$ 개일 때Permalink

$MSE(w_0,w_1,\cdots,w_K) = \dfrac{1}{n}\sum\limits_{i=1}^n (y_i - (w_0 + w_1x_{i1} + w_2x_{i2}+\cdots+w_Kx_{iK}))^2$

편미분을 하면 다음과 같다.

$\begin{aligned} \dfrac{\partial MSE}{\partial w_0} &= 2\dfrac{1}{n}\sum_i^n -(y_i-(w_0 + w_1x_{i1} + w_2x_{i2}+\cdots+w_kx_{iK}))\\\ \dfrac{\partial MSE}{\partial w_{1}} &= 2\dfrac{1}{n}\sum_i^n -x_{i1}(y_i-(w_0 + w_1x_{i1} + w_2x_{i2}+\cdots+w_kx_{iK}))\\\ \dfrac{\partial MSE}{\partial w_{2}} &= 2\dfrac{1}{n}\sum_i^n -x_{i2}(y_i-(w_0 + w_1x_{i1} + w_2x_{i2}+\cdots+w_kx_{iK}))\\\ &\vdots\\\ \dfrac{\partial MSE}{\partial w_{K}} &= 2\dfrac{1}{n}\sum_i^n -x_{iK}(y_i-(w_0 + w_1x_{i1} + w_2x_{i2}+\cdots+w_kx_{iK})) \end{aligned}$

의미 > $\hat{y}{i} = w_0 + w_1x{i1} + w_2x_{i2}+\cdots+w_kx_{iK}$ 일 때

$\dfrac{\partial MSE}{\partial w_0}$ : $-(y_i-\hat{y}_i)$ 들의 평균이다.
$\dfrac{\partial MSE}{\partial w_k},(k=1,\cdots,K)$ : $-x_{ik}(y_i-\hat{y}_i)$ 들의 평균이다.

이를 이용해서 추정하는 방법은 대표적으로 2가지이다.

1) 경사하강법(Gradient Descent)Permalink

IDEA! 기울기가 0이 될 때까지 계속 반복하면서 이동해보자.

그럼 어떻게 자동으로 이동시킬까? $\Rightarrow$ 기울기에 비례하게! 나도 설정할 수 있게!

기울기가 크다는 것은 아직 기울기가 0인 곳까지 도착하려면 멀었다는 의미 $\rightarrow$ 크게 움직이자.
기울기가 작다는 것은 곧 기울기가 0인 곳에 도착한다는 의미 $\rightarrow$ 작게 움직이자.
나도 움직임의 크기에 영향을 주고 싶다. $\rightarrow$ 학습률(learning rate) 등장

$\Rightarrow$ (학습률 $\times$ 기울기)만큼 움직이자!

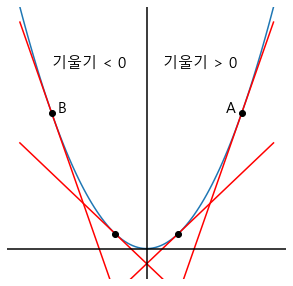
기울기가 +이면(A) 왼쪽(-)으로 이동
기울기가 -이면(B) 오른쪽(+)으로 이동

$\Rightarrow$ a = a - lr * (a일 때 기울기), b = b - lr * (b일 때 기울기)

STEP 1. 반복 횟수(epochs), 학습률(learning rate)과 초기값 $a, b$ 를 설정한다.
STEP 2. 예측값( $\hat{y}$ )을 계산한다. $\hat{y}_i = b + ax_i$
STEP 3. MSE를 계산한다. $MSE = (y - \hat{y})^2$
STEP 4. MSE의 기울기 값을 계산한다.
STEP 5. 새로운 a, b를 업데이트 한다.
STEP 6. STEP2 ~ STEP5을 epochs 만큼 반복

2) 최소제곱법(Least Square Method)Permalink

IDEA! 기울기를 0이라고 할 때 모수 값을 계산해보자.

설명변수가 한 개일 때Permalink

$\begin{aligned} \dfrac{\partial MSE}{\partial a} &= 2\dfrac{1}{n}\sum_i^n -x_i(y_i-(b+ax_i))=0\\ \dfrac{\partial MSE}{\partial b} &= 2\dfrac{1}{n}\sum_i^n -(y_i-(b+ax_i))=0 \end{aligned}$

Result

$\begin{aligned} b = \bar{y} - a\bar{x},\quad a = \dfrac{\sum\limits_{i=1}^n(x-\bar{x})(y-\bar{y})}{\sum\limits_{i=1}^n(x_i-\bar{x})^2} \end{aligned}$

증명(Click!)

(1) $b$ 추정하기

$\begin{aligned} 2\dfrac{1}{n}\sum_{i=1}^n -(y_i-(b+ax_i))&=0\\\ \dfrac{1}{n}\sum_{i=1}^n(y_i-b-ax_i)&=0\\\ b&= \dfrac{1}{n}\sum_{i=1}^n(y_i - ax_i)\\\ \therefore\;b&= \bar{y} - a\bar{x} \end{aligned}$

(2) $a$ 추정하기

$\begin{aligned} 2\dfrac{1}{n}\sum_{i=1}^n -x_i(y_i-(b+ax_i))&=0\\\ \dfrac{1}{n}\sum_{i=1}^n x_i(y_i-\bar{y}+\bar{y}-(b+ax_i-a\bar{x}+a\bar{x_i}))&=0\\\ \dfrac{1}{n}\sum_{i=1}^n x_i(y_i-\bar{y}-a(x_i-\bar{x_i})-b+\bar{y}-a\bar{x_i}))&=0\\\ \dfrac{1}{n}\sum_{i=1}^n x_i(y_i-\bar{y}-a(x_i-\bar{x_i}))&=0\quad (\because b= \bar{y} - a\bar{x})\\\ \dfrac{1}{n}\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y}-a(x_i-\bar{x_i}))&=0\quad (\because \text{편차의 합은 0})\\\ a\cdot \dfrac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2 &= \dfrac{1}{n}\sum_{i=1}^n(y_i-\bar{y})(x_i-\bar{x})\\\ \therefore\;a &= \dfrac{\sum\limits_{i=1}^n(x-\bar{x})(y-\bar{y})}{\sum\limits_{i=1}^n(x_i-\bar{x})^2} \end{aligned}$

설명변수가 $K$ 개일 때 (행렬로 계산)Permalink

※ 행렬의 미분

스칼라 $a^Tx$ 또는 $x^Ta$ 를 벡터 $x$ 로 미분하면 벡터 $a$

이차형식 $x^TAx$ 를 벡터 $x$ 로 미분하면 행렬 $(A+A^T)x$

벡터 $Ax$ 를 벡터 $x$ 로 미분하면 행렬 $A^T$

행렬의 미분(상세)(Click!)

(1) 스칼라를 벡터로 미분: Output > 열 벡터

$a=\begin{bmatrix}a_1\\ a_2\end{bmatrix}, x=\begin{bmatrix}x_1\\ x_2\end{bmatrix}$ 라고 하자.

$\begin{aligned} f &= a^Tx = x^Ta = a_1x_1 + a_2x_2 \\\ \dfrac{\partial f}{\partial x} &= \begin{bmatrix} \frac{\partial f}{\partial x_1} \\\ \frac{\partial f}{\partial x_2} \end{bmatrix} = \begin{bmatrix} a_1\\\ a_2 \end{bmatrix} = a \end{aligned}$

(2) 이차형식을 벡터로 미분: Output > 행렬

$A=\begin{bmatrix}a_{11}& a_{12}\\ a_{21} & a_{22}\end{bmatrix}, x=\begin{bmatrix}x_1\\ x_2\end{bmatrix}$ 라고 하자.

$\begin{aligned} f &= x^TAx = \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix}a_{11}& a_{12}\\\ a_{21} & a_{22}\end{bmatrix} \begin{bmatrix} x_1 \\\ x_2 \end{bmatrix}\\\ &= \begin{bmatrix} a_{11}x_1 + a_{21}x_2 & a_{12}x_1 + a_{22}x_2 \end{bmatrix} \begin{bmatrix} x_1 \\\ x_2 \end{bmatrix}\\\ &= a_{11}x_1^2 + a_{21}x_1x_2 + a_{12}x_1x_2 + a_{22}x_2^2\\\ \dfrac{\partial f}{\partial x}&= \begin{bmatrix} 2a_{11}x_1+a_{21}x_2 + a_{12}x_2\\\ a_{21}x_1+a_{12}x_1 +2a_{22}x_2 \end{bmatrix}= \begin{bmatrix} a_{11}x_1+a_{12}x_2+a_{11}x_1+a_{21}x_2\\\ a_{21}x_1+a_{22}x_2+a_{12}x_1+a_{22}x_2 \end{bmatrix}\\\ &=\left( \begin{bmatrix} a_{11} & a_{12}\\\ a_{21} & a_{22} \end{bmatrix} + \begin{bmatrix} a_{11} & a_{12}\\\ a_{21} & a_{22} \end{bmatrix}\right) \begin{bmatrix} x_1\\\ x_2 \end{bmatrix}= (A+A^T)x \end{aligned}$

(3) 벡터를 벡터로 미분: Output > 행렬

$A=\begin{bmatrix}a_{11}& a_{12}\\ a_{21} & a_{22}\end{bmatrix}, x=\begin{bmatrix}x_1\\ x_2\end{bmatrix}$ 라고 하자.

$\begin{aligned} f &= Ax = \begin{bmatrix}f_1 \\\ f2\end{bmatrix}= \begin{bmatrix} a_{11}x_1 + a_{12}x_2 \\\ a_{21}x_1 + a_{22}x_2 \end{bmatrix} \\\ \dfrac{\partial f}{\partial x} &= \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_2}{\partial x_1} \\\ \frac{\partial f_1}{\partial x_2} & \frac{\partial f_2}{\partial x_2} \end{bmatrix}= \begin{bmatrix} a_{11} & a_{21} \\\ a_{12} & a_{22} \end{bmatrix}= A^T \end{aligned}$

$\begin{aligned} MSE &= (y - Xw)^T(y-Xw) \\\ &= (y^T - w^TX^T)(y-Xw) \\\ &= y^Ty - w^TX^Ty - y^TXw + w^TX^TXw \\\ &= y^Ty - 2y^TXw + w^TX^TXw\quad(\because w^TX^Ty\text{는 스칼라이므로 전치행렬의 의미가 없다.}) \\\ &= y^Ty - (X^Ty)^Tw + w^TX^TXw \end{aligned}$

$\begin{aligned} \dfrac{\partial MSE}{\partial w} = -2X^Ty + 2X^TXw &= 0 \\\ \therefore\;w &= (X^TX)^{-1}X^Ty \end{aligned}$

Reference

데이터 사이언스 스쿨, link: https://datascienceschool.net

Twitter Facebook LinkedIn

Kim NaRae

[ML/DL] 선형 회귀분석

1. 회귀분석Permalink

1) 선형 회귀분석 / 비선형 회귀분석Permalink

선형 회귀분석Permalink

비선형 회귀분석Permalink

2) 단순 선형 회귀분석 / 다중 선형 회귀분석Permalink

단순 선형 회귀분석Permalink

다중 선형 회귀분석Permalink

2. 모수 추정Permalink

설명변수가 한 개일 때Permalink

설명변수가 $K$ 개일 때Permalink

1) 경사하강법(Gradient Descent)Permalink

2) 최소제곱법(Least Square Method)Permalink

설명변수가 한 개일 때Permalink

설명변수가 $K$ 개일 때 (행렬로 계산)Permalink

Reference

공유하기

댓글남기기

참고

[Git] Git 계정별 SSH Key 만들기

[Git] Git 명령어 모음

[GitHub] Discussion 관리

[GitHub] Readme 꾸미기 Tip 정리

Kim NaRae

1. 회귀분석Permalink

1) 선형 회귀분석 / 비선형 회귀분석Permalink

선형 회귀분석Permalink

비선형 회귀분석Permalink

2) 단순 선형 회귀분석 / 다중 선형 회귀분석Permalink

단순 선형 회귀분석Permalink

다중 선형 회귀분석Permalink

2. 모수 추정Permalink

설명변수가 한 개일 때Permalink

설명변수가 KK 개일 때Permalink

1) 경사하강법(Gradient Descent)Permalink

2) 최소제곱법(Least Square Method)Permalink

설명변수가 한 개일 때Permalink

설명변수가 KK 개일 때 (행렬로 계산)Permalink

Reference

공유하기

댓글남기기

참고

[Git] Git 계정별 SSH Key 만들기

[Git] Git 명령어 모음

[GitHub] Discussion 관리

[GitHub] Readme 꾸미기 Tip 정리

설명변수가 $K$ 개일 때Permalink

설명변수가 $K$ 개일 때 (행렬로 계산)Permalink