[Python Note] 넘파이(NumPy) 이해하기 (3)
1. 자료형(dtype)
연산이 가능한 이유?
Numpy에서 배열의 연산이 가능한 이유는 원소들이 모두 같은 자료형이기 때문이다.
| dtype | 설명 | dtype | 설명 |
|---|---|---|---|
b |
bool | i |
int |
f |
float | O |
object |
U |
string(유니코드) |
np.array(a, dtype='')
배열을 만들 때 자료형을 미리 설정할 수 있다.- 자료형을 알기 위해
type()을 썼던 것처럼.dtype()을 통해 배열의 자료형을 알 수 있다.
a = np.array([1, 2.2, 3])
b = np.array([1, 2.2, 3], dtype='i')
c = np.array([1, 2.2, 3], dtype='f')
d = np.array([1, 2.2, 3], dtype='O')
e = np.array([1, 2.2, 3], dtype='U')
a > [1. 2.2 3. ] float64
b > [1 2 3] int32
c > [1. 2.2 3. ] float32
d > [1 2.2 3] object
e > ['1' '2.2' '3'] <U3
2. 벡터화 연산
벡터화 연산이란 같은 위치의 원소끼리 연산이 되므로,
연산하기 위해서는 벡터 또는 행렬의 크기가 같아야한다.
1) Math Function
import numpy as np
| 함수 | 설명 |
|---|---|
np.add(arr1, arr2) |
같은 위치의 원소끼리 덧셈 |
np.multiply(arr1, arr2) |
같은 위치의 원소끼리 곱셈 |
np.sqrt(x) |
각 원소에 대해 $\sqrt{x}$ |
np.exp(x) |
각 원소에 대해 $e^x$ |
np.log(x) |
각 원소에 대해 $\log_e(x), x>0$ |
로그함수의 경우 밑의 값에 따라 np.log10(x), np.log2(x)를 사용할 수 있다. |
- 그 외의 함수들은 다음을 참고하자. NumPy Manual
2) Inf / NaN
np.inf(): infinity(무한대)
ex. $\lim\limits_{x\to \infty} e^x = \infty$, $1 / 0 = \infty$np.nan(): Not a Number ex. $0/0$, $\log(-1)$
a = np.array([1])
b = np.array([0])
print('inf >', np.inf)
print('1/inf >', 1 / np.inf)
print('NaN >', np.nan)
print('log(-1) >', np.log(-1))
print('1/0 >', a/b)
print('0/0 >', b/b)
inf > inf
1/inf > 0.0
NaN > nan
log(-1) > nan
1/0 > [inf]
0/0 > [nan]
3) 스칼라 연산(브로드캐스팅)
- 브로드캐스팅(Broadcasting)
벡터 또는 행렬의 각 원소에 스칼라의 연산으로 계산된다.
\[ \begin{bmatrix} 1\\ 2\\ 3\\ 4 \end{bmatrix} \times 2 = \begin{bmatrix} 1\times 2\\ 2\times 2\\ 3\times 2\\ 4\times 2 \end{bmatrix} \]
- 고차원에서 작은 차원의 행 또는 열이 같아도 적용될 수 있다.
\[ \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ 10 & 11 & 12 \end{bmatrix} + \begin{bmatrix} 1\\ 2\\ 3\\ 4\end{bmatrix} = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ 10 & 11 & 12 \end{bmatrix} + \begin{bmatrix} 1 & 1 & 1\\ 2 & 2 & 3\\ 3 & 3 & 3\\ 4 & 4 & 4\end{bmatrix} \]
\[ \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ 10 & 11 & 12 \end{bmatrix} + \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9\\ 10 & 11 & 12 \end{bmatrix} + \begin{bmatrix} 1 & 2 & 3\\ 1 & 2 & 3\\ 1 & 2 & 3\\ 1 & 2 & 3 \end{bmatrix} \]
arr1 = np.arange(1,5)
arr2 = np.arange(1,13).reshape(4, 3)
arr3 = np.arange(1, 5).reshape(4, 1)
arr4 = np.arange(1, 4).reshape(1, 3)

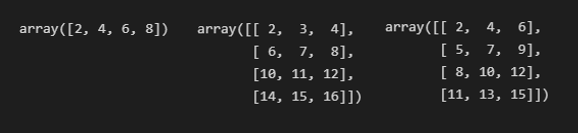
arr1 * 2
arr2 + arr3
arr2 + arr4
4) 벡터 연산
- 같은 위치에 있는 원소들끼리 대해 연산한다.
- For문으로 각 원소들마다 연산을 하는 것보다 훨씬 빠르다.
- For문
%%time arr1 = np.arange(1, 1001) arr2 = np.arange(1001, 2001) arr3 = np.zeros_like(arr1) for i in range(len(arr1)): arr3[i] = arr1[i] + arr2[i]Wall time: 2 ms - 배열의 연산
%%time arr1 = np.arange(1, 1001) arr2 = np.arange(1001, 2001) arr3 = arr1 + arr2Wall time: 0 ns
- For문
5) 논리 연산
>,<,==,!=등 논리 연산자도 같은 위치의 원소에 대해 적용된다.np.all()은 논리 연산 결과가 모두True일 때True, 아니면False를 반환한다.
arr1 = np.array([1, 3, 5, 4, 2])
arr2 = np.array([2, 3, 1, 4, 5])
arr1 == arr2
array([False, True, False, True, False])
6) 차원 축소 연산
- 행 또는 열에 대해 합, 평균을 구하면 각 행 또는 열에 대해 하나의 숫자로 계산된다. 이러한 연산을 차원 축소(dimension reduction) 연산이라고 한다.
axis=0은 열,axis=1은 행에 대해 계산한다.- 표본에 대한 분산, 표준편차의 경우
ddof=1옵션을 추가한다.
($s^2$: 분산, $s$: 표준편차)- $s^2 = \dfrac{1}{N}\sum\limits_{i=1}^N(x_i-\bar{x})^2,\quad s^2 = \dfrac{1}{N-1}\sum\limits_{i=1}^N(x_i-\bar{x})^2$
함수 설명 함수 설명 arr.min()
np.min(arr)최솟값 arr.max()
np.max(arr)최댓값 arr.argmin()
np.argmin(arr)최솟값 위치 arr.argmin()
np.argmin(arr)최댓값 위치 arr.sum()
np.sum(arr)합계 arr.mean()
np.mean(arr)평균 np.median(arr)중앙값 arr.var()
np.var(arr)분산 arr.std()
np.std(arr)표준편차 np.quandtile(arr,perc)
np.percentile(arr, perc)사분위수 '논리'.all()
np.all('논리')논리가 모두
True인가'논리'.all()np.any('논리')논리가 하나라도
True인가
# 통계 1 - 합계
arr1 = np.arange(1,13).reshape(3,4)
arr1
arr1.sum()
arr1.sum(axis=0) # 각 열에 대해 계산
arr1.sum(axis=1) # 각 행에 대해 계산
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
78
array([15, 18, 21, 24])
array([10, 26, 42])
# 통계 2 - 사분위수
arr2 = np.arange(10)
arr2
np.quantile(arr2, [0.0, 0.25, 0.5, 0.75, 1])
np.percentile(arr2, [0, 25, 50, 75, 100])
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
array([0. , 2.25, 4.5 , 6.75, 9. ])
array([0. , 2.25, 4.5 , 6.75, 9. ])
# 논리 연산
arr1 = np.array([1, 3, 2, 4, 5])
arr2 = np.array([1, 2, 3, 4, 5])
arr3 = np.array([1, 3, 2, 4, 5])
print('arr1 == arr2 >', arr1 == arr2)
print('np.all(arr1 == arr2) >', (arr1 == arr2).all())
print('np.all(arr1 == arr3) >', (arr1 == arr3).all())
print('np.any(arr1 == arr2) >', (arr1 == arr2).any())
print('np.any(arr1 == arr3) >', (arr1 == arr3).any())
arr1 == arr2 > [ True False False True True]
np.all(arr1 == arr2) > False
np.all(arr1 == arr3) > True
np.any(arr1 == arr2) > True
np.any(arr1 == arr3) > True
3. 정렬
arr.sort()또는np.sort(arr)로 정렬할 수 있다.
arr.sort()은 배열arr의 값이 바뀌고, 출력되지 않는다.
np.sort(arr)는 바뀌지 않고 출력된다.arr.argsort()또는np.argsort(arr)로 원소의 순서(rank)를 알 수 있다.
해당 자리에 와야할 원소의 현재 위치를 반환한다.axis=0은 열,axis=1은 행에 대해 정렬한다.
지정하지 않으면 가장 안쪽의 차원에 대해 정렬한다.
arr1 = np.array([[13, 24, 3, 54],
[24, 31, 54, 2],
[14, 1, 35, 21]])
arr1
np.sort(arr1, axis=0)
np.sort(arr1, axis=1)

arr1
np.sort(arr1, axis=1)
np.argsort(arr1, axis=1)




댓글남기기